Автор: Евгений Бодягин, https://dsprog.pro
Введение
Необходимо проанализировать эффективность нового дизайна для сайта. Располагаем данными о пользователях сайта со значением конверсии по каждому пользователю/сеансу. Проведем A-B тест. Прежнюю форму дизайна назовем «А»; новую форму дизайна назовем «B».
Дизайн эксперимента
- Нулевая гипотеза: Нет разницы в эффективности между дизайном A и B.
- Альтернативная гипотеза: Есть значительная разница в эффективности между дизайном A и B.
- Объект обработки: Две выборки сеансов посетителей сайта перемешанные случайным образом. Размер выборок одинаков.
- Целевая аудитория: Посетители сайта за последние 40 дней.
- Метрики: Impressions, Clicks, Purchase, Earning
- Длительность проведения теста: 40 дней.
- Уровни значимости:
- α = 0.05
- β = 0.2
- Кампании запускаются одновременно, а аудитория делится случайным образом.
Структура данных
- Название кампании (Campaign Name): Название кампании.
- Показы (Impression): Количество показов рекламы.
- Клики (Click): Количество кликов на баннер и перешли на сайт.
- Покупки (Purchase): Сколько раз пользователи совершили покупку.
- Прибыль (Earning): Прибыль после покупки товаров.
import itertools
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import statsmodels.stats.api as sms
from scipy.stats import ttest_1samp, shapiro, levene, ttest_ind, mannwhitneyu, pearsonr, spearmanr, kendalltau,
f_oneway, kruskal
# this content is from dsprog.pro
from statsmodels.stats.proportion import proportions_ztest
pd.set_option('display.max_columns', None)
pd.set_option('display.max_rows', 10)
pd.set_option('display.float_format', lambda x: '%.5f' % x)
Определение уровней: значимость теста и мощность теста
import scipy # Significance level (Probability of Type I error) that is used to decide whether to reject the null hypothesis. alpha = 0.05 # Power of the test (probability of type II error), which indicates the probability of not detecting a real effect when it exists. beta = 0.2
Загрузка данных
Эксперимент проводился в течение 40 дней. Загрузим имеющиеся данные.
a_group = pd.read_csv('input/Xa_group.csv', delimiter=',')
a_group.head()
| Campaign Name | Impression | Click | Purchase | Earning | |
|---|---|---|---|---|---|
| 0 | a campaign | 77198 | 4774 | 307 | 1933 |
| 1 | a campaign | 126169 | 4285 | 574 | 2572 |
| 2 | a campaign | 114917 | 4134 | 720 | 2212 |
| 3 | a campaign | 133553 | 5144 | 545 | 1957 |
| 4 | a campaign | 90761 | 1948 | 186 | 1675 |
b_group = pd.read_csv('input/Xb_group.csv', delimiter=',')
b_group.head()
| Campaign Name | Impression | Click | Purchase | Earning | |
|---|---|---|---|---|---|
| 0 | b campaign | 115507 | 1942 | 656 | 2335 |
| 1 | b campaign | 130944 | 2844 | 606 | 2748 |
| 2 | b campaign | 175336 | 2953 | 287 | 3690 |
| 3 | b campaign | 139732 | 3550 | 709 | 2184 |
| 4 | b campaign | 108745 | 3261 | 297 | 2454 |
desired_palette = ["#0099cc", "#009900"]
data_all = pd.concat([a_group, b_group])
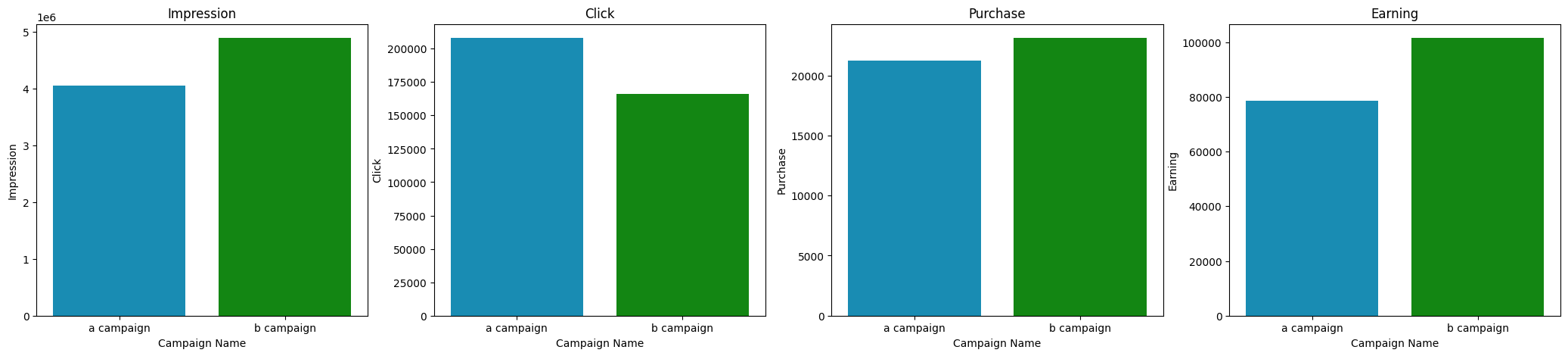
fig, ax = plt.subplots(ncols=4, figsize=(26,5))
ax1 = sns.barplot(data=data_all, x='Campaign Name', y='Impression', errorbar=('ci', False), ax=ax[0], estimator='sum', palette=desired_palette)
ax2 = sns.barplot(data=data_all, x='Campaign Name', y='Click', errorbar=('ci', False), ax=ax[1], estimator='sum', palette=desired_palette)
ax4 = sns.barplot(data=data_all, x='Campaign Name', y='Purchase', errorbar=('ci', False), ax=ax[2], estimator='sum', palette=desired_palette)
ax5 = sns.barplot(data=data_all, x='Campaign Name', y='Earning', errorbar=('ci', False), ax=ax[3], estimator='sum', palette=desired_palette)
# this content is from dsprog.pro
ax1.set_title('Impression')
ax2.set_title('Click')
ax4.set_title('Purchase')
ax5.set_title('Earning')
plt.show()
Дорожная карта формулировки гипотез
- Предположение того, что данные распределены нормально (нормальность)
- Предположение того, что дисперсия однородна (гомогенность).
Оба предположения будут проверены посредством критерия статистической значимости. Вид тестов, будет выбран для каждой задачи. Если оба предположения допустимы, применим два независимых выборочных t-теста. Если одно из предположений можно отклонить, будет применен критерий U-критерий Манна — Уитни (непараметрический критерий).
Замечание: t-критерий используется для проверки существования статистически значимой разницы между двумя группой A и группой B путем рассмотрения средних значений. Это параметрический тест.
Тест Шапиро-Уилка
Существует большое количество тестов на нормальность. Наиболее известными из них являются критерий:
- критерий хи-квадрат;
- критерий Колмогорова-Смирнова;
- критерий Лиллиефорса;
- критерий нормальности Шапиро-Уилка. Используем последний из них.
Unable to reject Null Hypothesis for «Impression» in «group A», because «Test Stat group A» = 0.9810 and «p-value_a» = 0.7250 Unable to reject Null Hypothesis for «Impression» in «group B», because «Test Stat group B» = 0.9609 and «p-value_b» = 0.1801
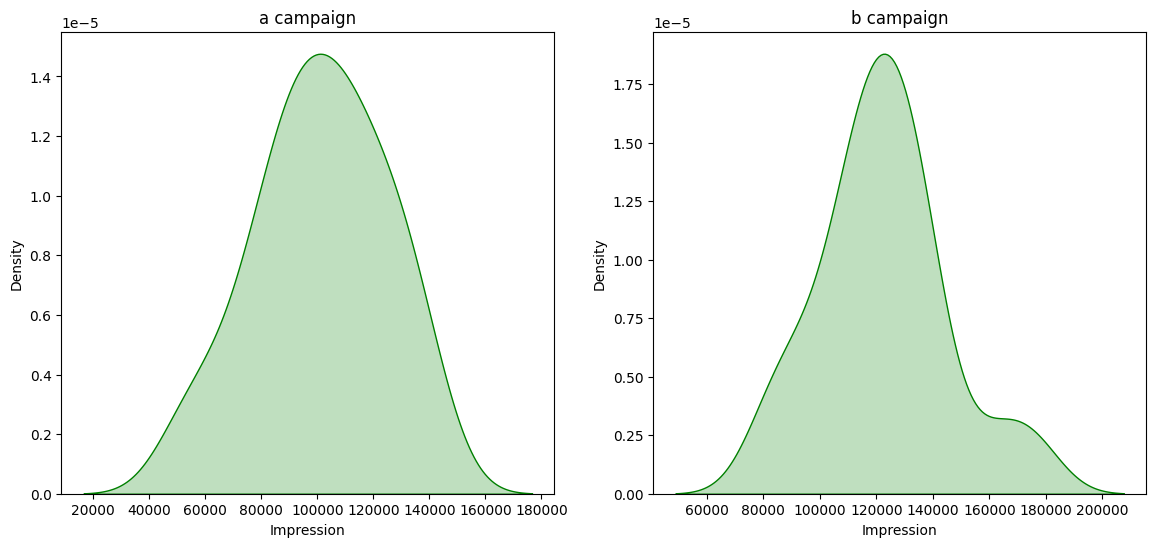
Unable to reject Null Hypothesis for «Click» in «group A», because «Test Stat group A» = 0.9882 and «p-value_a» = 0.9465 Unable to reject Null Hypothesis for «Click» in «group B», because «Test Stat group B» = 0.9709 and «p-value_b» = 0.3851

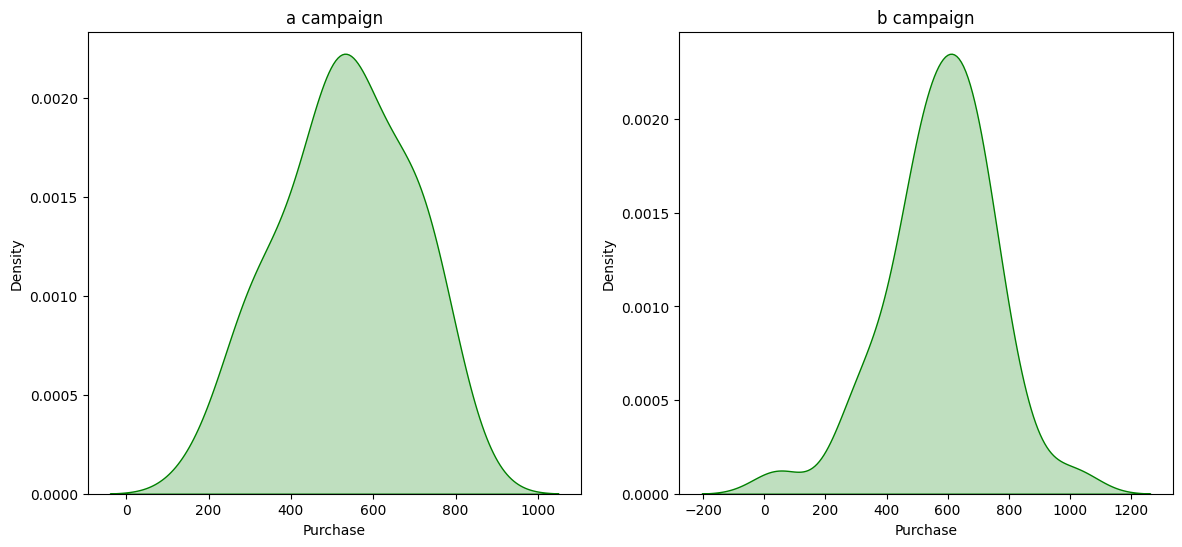
Unable to reject Null Hypothesis for «Purchase» in «group A», because «Test Stat group A» = 0.9775 and «p-value_a» = 0.5972
Unable to reject Null Hypothesis for «Purchase» in «group B», because «Test Stat group B» = 0.9690 and «p-value_b» = 0.3341
Unable to reject Null Hypothesis for «Earning» in «group A», because «Test Stat group A» = 0.9790 and «p-value_a» = 0.6524 Unable to reject Null Hypothesis for «Earning» in «group B», because «Test Stat group B» = 0.9734 and «p-value_b» = 0.4570

Итак. Ни по одному из показателей: Impression, Click, Purchase нельзя отвергнуть нулевую гипотезу о нормальности распределения.
Тест Левена
Проводим тест Левена, чтобы проверить, есть ли значимые различия в вариациях между группами.
columns = ["Impression", "Click", "Purchase", "Earning"]
for column in columns:
test_stat, pvalue = levene(a_group[column], b_group[column])
if (pvalue < alpha):
print('Reject Null Hypothesis for "%s" because "Test Stat" = %.4f and "p-value" = %.4f ' % (column, test_stat, pvalue))
else:
print('Unable to reject Null Hypothesis for for "%s" because "Test Stat" = %.4f and "p-value" = %.4f ' % (column, test_stat, pvalue))
Unable to reject Null Hypothesis for for «Impression» because «Test Stat» = 0.5893 and «p-value» = 0.4450
Unable to reject Null Hypothesis for for «Click» because «Test Stat» = 0.0978 and «p-value» = 0.7553
Unable to reject Null Hypothesis for for «Purchase» because «Test Stat» = 0.0232 and «p-value» = 0.8793
Unable to reject Null Hypothesis for for «Earning» because «Test Stat» = 0.2993 and «p-value» = 0.5859
Итак. Ни по одному из показателей: Impression, Click, Purchase нельзя отвергнуть нулевую гипотезу об отсутствии значимых различий в вариациях между группами.
В соответствие с определенной выше дорожной картой формулировки гипотез это означает, что можем применить два независимых выборочных T-теста.
T тест
columns = ["Impression", "Click", "Purchase", "Earning"]
for column in columns:
test_stat, pvalue = ttest_ind(a_group[column], b_group[column], equal_var=True)
if (pvalue < alpha):
# this content is from dsprog.pro
print('Reject Null Hypothesis for "%s" because "Test Stat" = %.4f and "p-value" = %.4f ' % (column, test_stat, pvalue))
else:
print('Unable to reject Null Hypothesis for for "%s" because "Test Stat" = %.4f and "p-value" = %.4f ' % (column, test_stat, pvalue))
Reject Null Hypothesis for «Impression» because «Test Stat» = -4.1173 and «p-value» = 0.0001
Reject Null Hypothesis for «Click» because «Test Stat» = 2.7901 and «p-value» = 0.0066
Unable to reject Null Hypothesis for for «Purchase» because «Test Stat» = -1.2474 and «p-value» = 0.2160
Reject Null Hypothesis for «Earning» because «Test Stat» = -7.0324 and «p-value» = 0.0000
Итак, с помощью t-критерия определили единственный параметр (Purchase), который не имеет статистически значимую разницу между группой A и группой B. По остальным параметрам возможно отклонить нулевую гипотезу.
Промежуточный итог
Учитывая то, что все показатели имеют нормальное распределение, а также отсутствие значимых различий в вариациях между группами, возможно завершить процесс обработки данных.
Вывод таков. Новый дизайн B оказывает влияние на показатели:
- Impression,
- Click,
- Earning
Новый дизайн B не оказывает влияния на показатель:
- Purchase
Однако, возможно создать комбинированную функцию которая с учетом нормальности, значимости вариаций использовала либо не использовала критерий U-критерий Манна — Уитни (непараметрический критерий)
U-критерий Манна — Уитни в обработке данных
columns = ["Impression", "Click", "Purchase", "Earning"]
for column in columns:
hypothesis_checker(a_group, b_group, column)
========== Impression ==========
*Normalization Check:
Shapiro Test for Control Group, Stat = 0.9810, p-value = 0.7250
Shapiro Test for Test Group, Stat = 0.9609, p-value = 0.1801
*Variance Check:
Levene Test Stat = 0.5893, p-value = 0.4450
Independent Samples T Test Stat = -4.1173, p-value = 0.0001
H0 hypothesis REJECTED, Independent Samples T Test
========== Click ==========
*Normalization Check:
Shapiro Test for Control Group, Stat = 0.9882, p-value = 0.9465
Shapiro Test for Test Group, Stat = 0.9709, p-value = 0.3851
*Variance Check:
Levene Test Stat = 0.0978, p-value = 0.7553
Independent Samples T Test Stat = 2.7901, p-value = 0.0066
H0 hypothesis REJECTED, Independent Samples T Test
========== Purchase ==========
*Normalization Check:
Shapiro Test for Control Group, Stat = 0.9775, p-value = 0.5972
Shapiro Test for Test Group, Stat = 0.9690, p-value = 0.3341
*Variance Check:
Levene Test Stat = 0.0232, p-value = 0.8793
Independent Samples T Test Stat = -1.2474, p-value = 0.2160
H0 hypothesis NOT REJECTED, Independent Samples T Test
========== Earning ==========
*Normalization Check:
Shapiro Test for Control Group, Stat = 0.9790, p-value = 0.6524
Shapiro Test for Test Group, Stat = 0.9734, p-value = 0.4570
*Variance Check:
Levene Test Stat = 0.2993, p-value = 0.5859
Independent Samples T Test Stat = -7.0324, p-value = 0.0000
H0 hypothesis REJECTED, Independent Samples T Test
Результаты комбинированной функции ничем не отличаются от ранее оглашенных промежуточных выводов. Однако в ней есть потенциал для расчета случаев, когда непараметрический критерий необходим.
Выводы
Оба варианта дизайна A и B характеризуются показателями «Impression», «Click», «Purchase», «Earning».
Ни по одному из показателей: Impression, Click, Purchase нельзя отвергнуть нулевую гипотезу о нормальности распределения.
Ни по одному из показателей: Impression, Click, Purchase нельзя отвергнуть нулевую гипотезу об отсутствии значимых различий в вариациях между группами.
Данные два факта позволили применить параметрический T-тест.
В результате проведения данного теста было выявлено, что лишь единственный параметр (Purchase), не имеет статистически значимую разницу между группой A и группой B.
Таким образом, существует значительная разница в эффективности между вариантами дизайна A и B.
Дополнительно была создана комбинированная функцию которая с учетом нормальности, значимости вариаций использует либо не использует U-критерий Манна — Уитни (непараметрический критерий). В ней есть потенциал для расчета случаев, когда непараметрический критерий необходим.
=======================
Для получения полного контента данной статьи; для сотрудничества с автором, пишите в Телеграм: cryptosensors
Полный контент данной статьи включает файлы/данные:
- файл Jupyter Notebook (ipynb),
- файлы датасетов (csv или xlsx),
- неопубликованные элементы кода, нюансы.
Распространение материалов с dsprog.pro горячо приветствуется (с указанием ссылки на источник).



